

To best showcase the difference between the windowing function, the original configuration is recommended. Note, that this configuration may produce different designs. %Number of iterations to average the objective %Iteration number to begin the reverse time integration in the direct solver for the unsteady adjoint. Here we set ITER_AVERAGE_OBJ=TIME_ITER-WINDOW_START_ITER=700. The time to average the objective and constraint function is given by the option ITER_AVERAGE_OBJ. We set the start iteration to the final iteration of the direct run, i.e. it starts at iteration given by UNST_ADJOINT_ITER and ends at iteration 0. Note, that the adjoint iterator runs backwards in time, i.e.
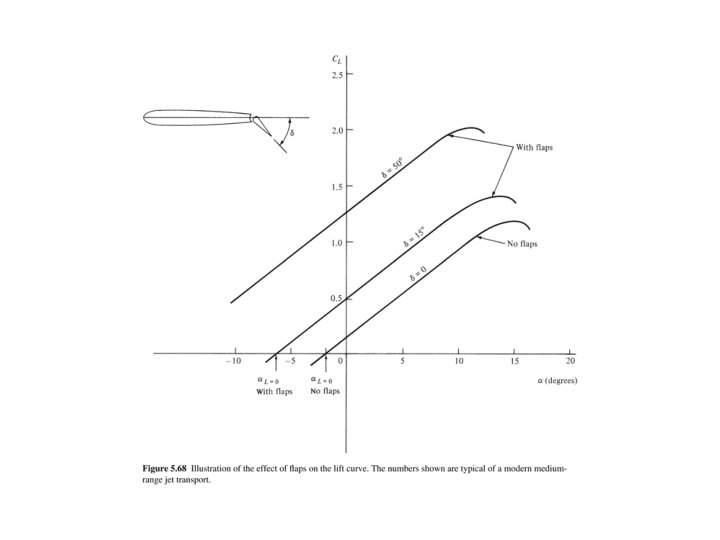
Make sure that the option INNER_ITER is chosen big enough in your test case to get It may happen that the adjoint inner iterator needs more iterations to reach a steady state. Asymptotically, the convergence speed of the adjoint inner iteration matches the speed of the direct inner iteration. To the one used for the direct simulation. This means, sensitivies are calculated using a dual time-stepping method similar To compute the sensitivity of the optimization objective and constraint, SU2 uses an adjoint iterator. Options (SQUARE, HANN, HANN_SQUARE, BUMP), SQUARE is default. % Window-function to weight the time average. % Iteration to start the windowed time average More information about setting up unsteady simulations can be found here To compute the unsteady shape optimization, we set up the unsteady simulation according to our test case above. The period average is approximated by a windowed time-average over a finite time-span \(M\) A meaningful objective and constraint function is therefore a time average over a period. We want to solve an optimization problem with a time dependent system output, e.g. These subsonic flow conditions will cause a detached flow about the airfoil, that exhibts a vortex street and is therefore periodic for the baseline geometry.ĭepending on the windowing-function used to average the optimization objective, the flow about the optimized geometry will eventually be a steady state flow.

#Airfoil shape series#
The NACA-4-Digit series is a set of 78 airfoil configurations which were created for wind-tunnel tests to explore the effect of different airfoil shapes on aerodynamic coefficients as drag or lift. The NACA airfoils are two dimensional shapes for aircraft wings developed by the National Advisory Committee for Aeronautics (NACA, 1915-1958, predecessor of NASA). This test case is for the NACA0012 airfoil in viscous unsteady flow.
#Airfoil shape download#
If you have yet to complete these requirements, please see the Download and Installation pages. To this end, it is assumed you have already obtained and compiled SU2_CFD and its adjoint capabilities. The tutorial will also address procedures for parallel computations. The following tutorial will walk you through the steps required when performing a shape optimization of the NACA0012 airfoil using SU2.
#Airfoil shape how to#
For more information on how to set up an FFD-Box on your own, please follow this tutorial. The used mesh already contains an FFD-Box. The mesh file ( unsteady_naca0012_FFD.su2). You will need the configuration file ( unsteady_naca0012_opt.cfg) and The resources for this tutorial can be found in theĭesign/Unsteady_Shape_Opt_NACA0012 directory Hence it is recommended to read that tutorial first. This tutorial uses the windowing techniques explained in here, to compute meaningful optimization objectives. The specific geometry chosen for the tutorial is the classic NACA0012 airfoil.Ĭonsequently, the following capabilities of SU2 will be showcased in this tutorial. Upon completing this tutorial, the user will be familiar with perfoming an optimization of a viscous, unsteady, periodic flow about It is assumed, that the user is familiar with the shape optimization capabilities of SU2 in steady state flows, which are explained in Figure (1): Baseline NACA0012 airfoil (left), optimized design using Square-windowing (middle) and optimized design using Hann-Square-windowing (right).


 0 kommentar(er)
0 kommentar(er)
